【置顶说明】
本卡组自上架以来已经历三个年头,综合考虑到自己上岸已过多年与个人目前的精力等因素,能够为大家提供的售后(包含经验贴与知识总结等)可能已经较为滞后,因此自2024年9月1日起本卡组及本人在售卡组不再提供售后微信联系方式(但本卡组为各位提供的价值和思路借鉴足以匹配这份并不贵的定价),待有时间启动大版本更新后会第一时间提价并恢复售后。
再次感谢你的理解和支持!诚挚的祝愿你考试成功!
【调价说明】
自考研上岸以来,现在的我是即将研究生毕业准备开启人生下一阶段的准打工人。很开心在anki记忆卡软件与平台还尚未如现在这般壮大前便在此分享我自制的卡组,自卡组上线以来共超过1300人次下载使用。现在平台靠会员体系完善了资金来源并保障了其运行良性循环;与此同时,时过境迁,由于研究生阶段的学习深耕使得该卡组的更新可能也并不能完全适应现在的考研备考。所以,自2024年1月1日起,决定对本卡组进行调价(本卡组调价前24.99RMB,调价后定价为:2.99RMB),倘若这份卡组还能对你的备考路途有一定启发,那将是这份卡组的荣幸!祝你也顺利上岸!
PS.购买卡组后将享受本卡组的终身更新,倘若我仍有余力推陈出新并再次调价,您依旧将对本卡组享受终身免费更新。
【旧说明】
本卡组属自用分享,精校对无卡组水印高质量,愿使用卡组的朋友也可以吸到我的好运成功上岸!学习是效率至上的事情,希望卡组代替我作为领学人视角带你直接学习最有用的,前人栽树后人乘凉,而不是胡子眉毛一把抓的......
烦请阅读下方卡组简介与使用说明,购买卡组后可添加微信获取赠送的资料,资料价值或许远超卡组本身价格,所以请购买之后一定要记得联系我!资料如下:
1.243分上岸211初试攻略(含各科用书与网课评价及备考时间规划等)
2.管综考研历年真题模考情况EXCEL表格(可通过该表对照评估自身实际实力水平)
3.原创初级会计与CMA一次性通过攻略
4.超4000字原创CPA经济法+CPA战略备考攻略(含跟课老师、备考时间、历年真题模拟情况与无纸化学习思路方法等),并可专享免拼团购买拼团价CPA卡组资格。
5.大佬室友一次性通过4科CPA的攻略
*未来可能会有的事务所实习经验贴与找工作注意事项等交流
注:
1.可通过作者其他卡组中找寻“《置身事内》读书笔记”“公司治理”两份免费卡组体验我的制卡风格!
2.由于IOS抽成问题,请IOS用户购卡前联系微信后再购买,感谢支持!
3.微信号为本人自用号并非营销号,并且碍于平时比较忙,微信回复慢还请见谅。
【卡组简介】
2021成功上岸某211,为了做到与时俱进,更新了2021年我当时考试时的考场错题与解析!(公式部分用了mathjax所以会比贴图更好看一点~),制作不易!!(我都是把卡组当自己孩子用心做的!)
卡组的主要内容如下(共计382张):

卡组分为知识点、错题集和真题集三个部分,里面图片较多但是绝对保证清晰,我的建议是手机背诵知识点,平板刷题。
知识点部分依托老吕和陈剑的参考书PDF整合做的,拆分的很小很细的,重点的话我自己有黄色高亮标注,图片可能有一点不那么影响阅读的水印(强迫症勿扰);
【卡组预览】


错题集是我自己做的《老吕800》《高分指南》的错题整理(里面大多是易错题和难题),真题是我自己做的真题错题整理。


最后还有我自己在考前最后一轮整理的查漏补缺也在其中。
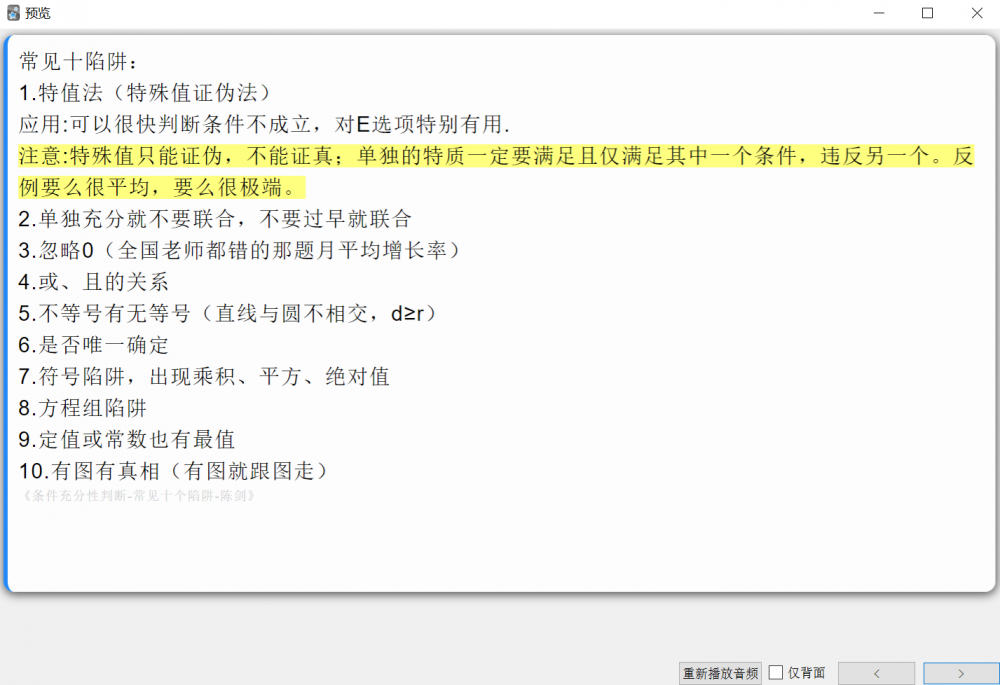

总之是陪着自己走完整个专硕考研备考全程的自制卡组惹,呜呜呜,好好爱惜它!
 MissTime 更新日期:2024-08-31 14:41:45
MissTime 更新日期:2024-08-31 14:41:45








 考神背多分
考神背多分
 ANKI小助手
ANKI小助手