🌟26考公考编全套【数量/资料/成语/图推/类比/政治/常识/申论】
公务员事业编选调生通用
国考省考事业单位
行测笔试
考证/考公/职考 / 行测
⭐全套笔记卡组.apkg
¥239元
408.6MB
| 🔥
|
兑换码
5 评分
 云深制卡 更新日期:2025-07-02 15:14:44
云深制卡 更新日期:2025-07-02 15:14:44
购买须知:此交易为您和其他用户的交易,作为公益平台,资源网不参与任何交易抽成和收费行为,如您对资源有疑问请联系作者,如无法联系作者可联系平台为您提供帮助
作者已提供售后联系方式,购买后可见
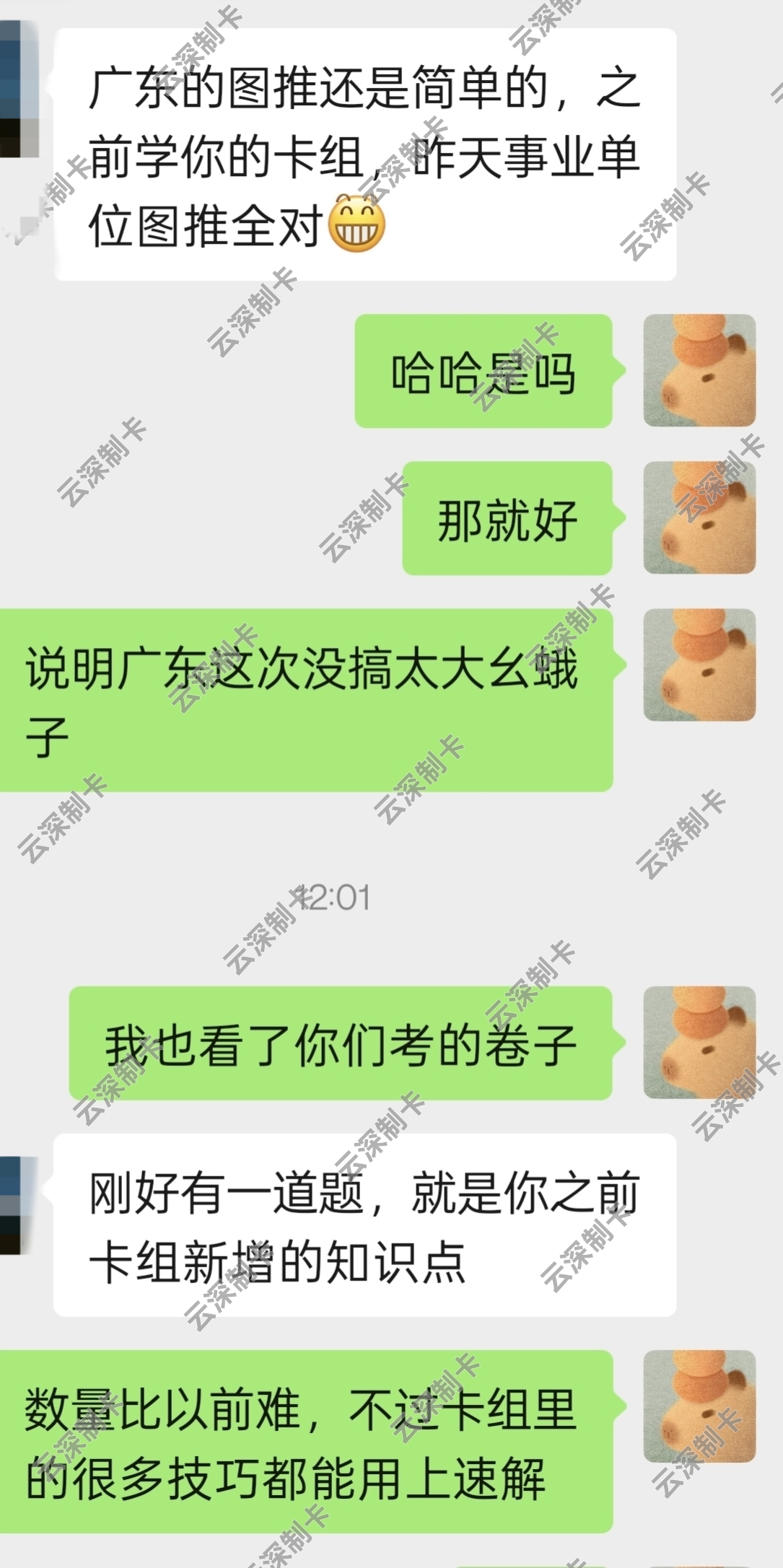
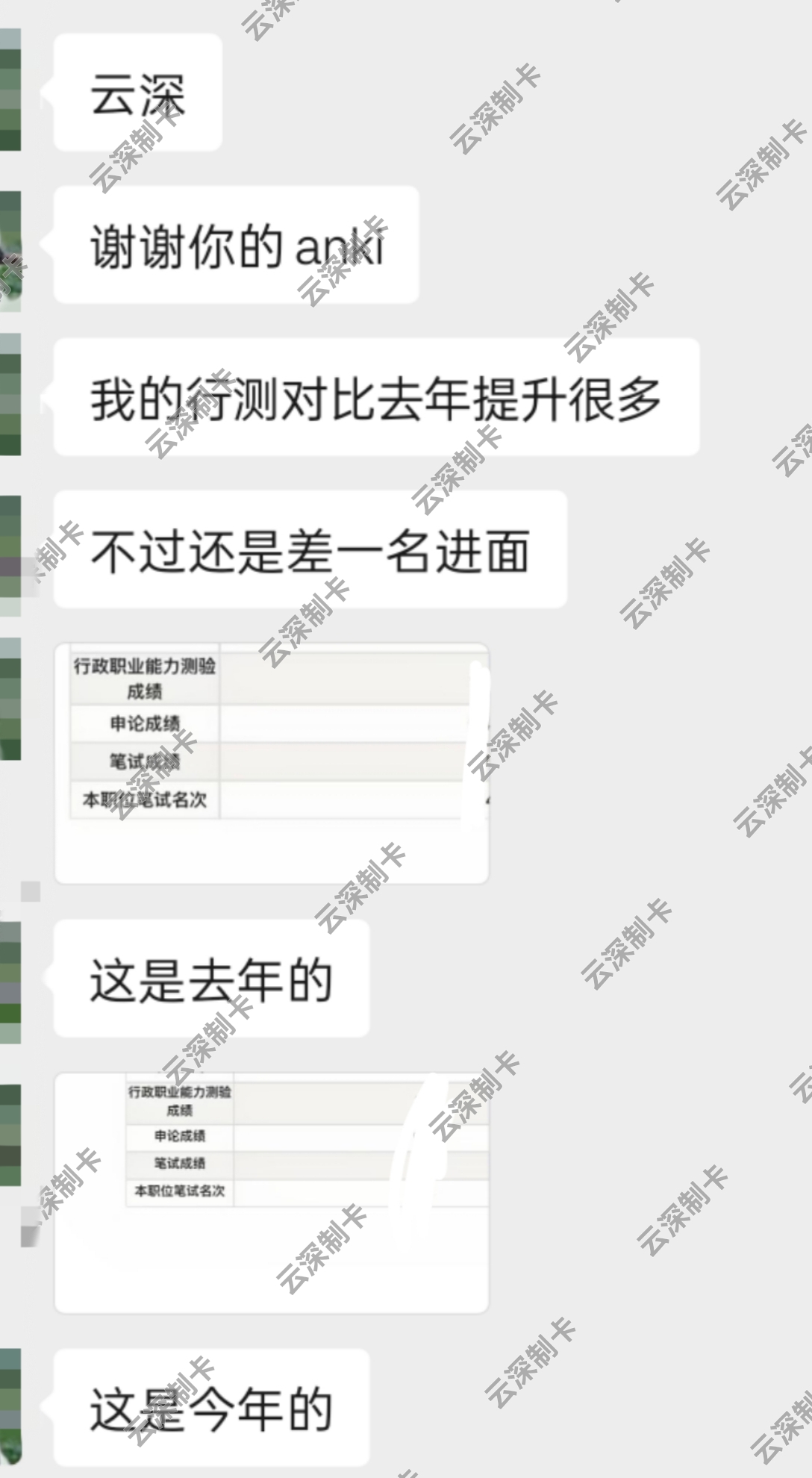
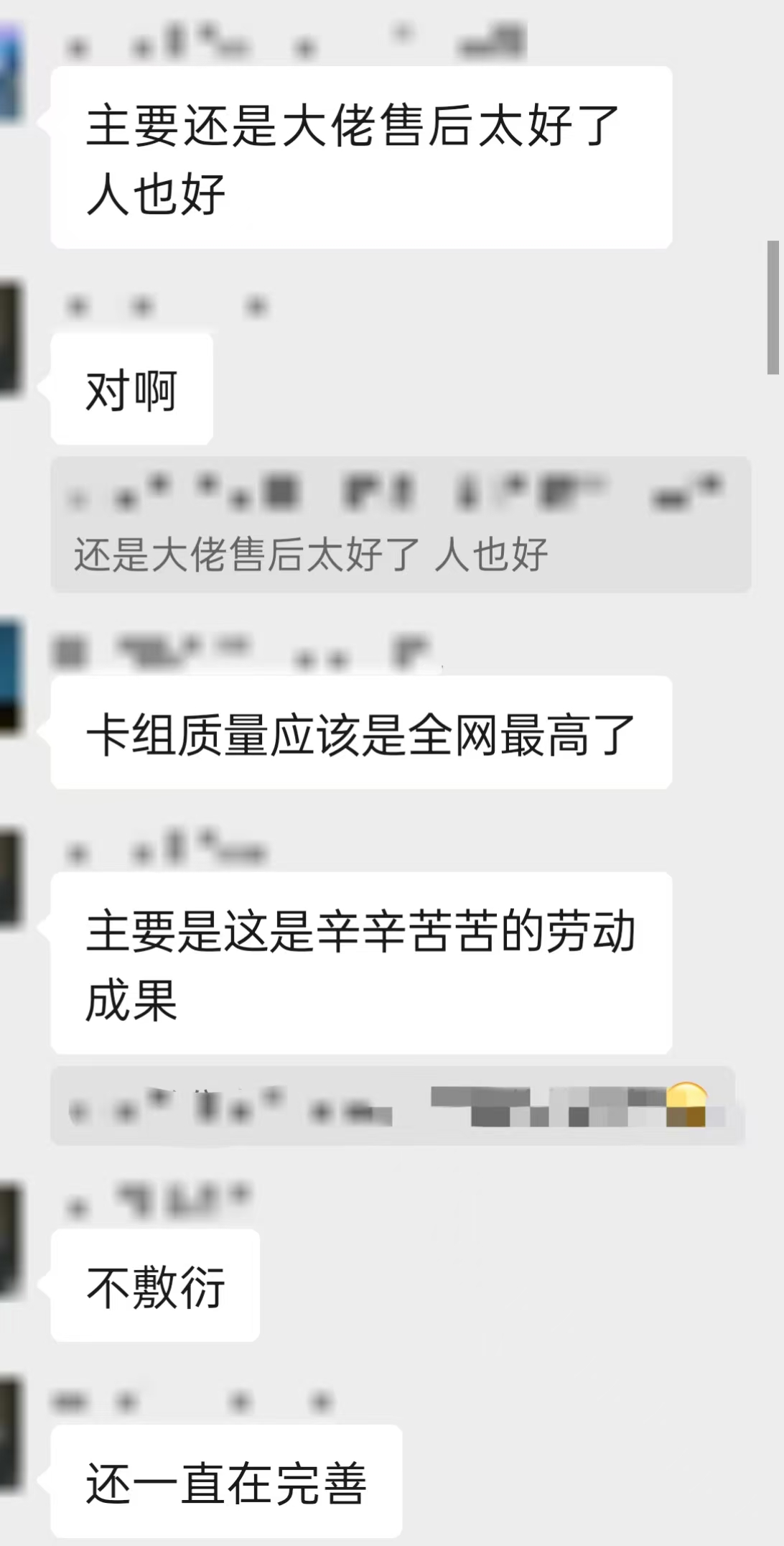
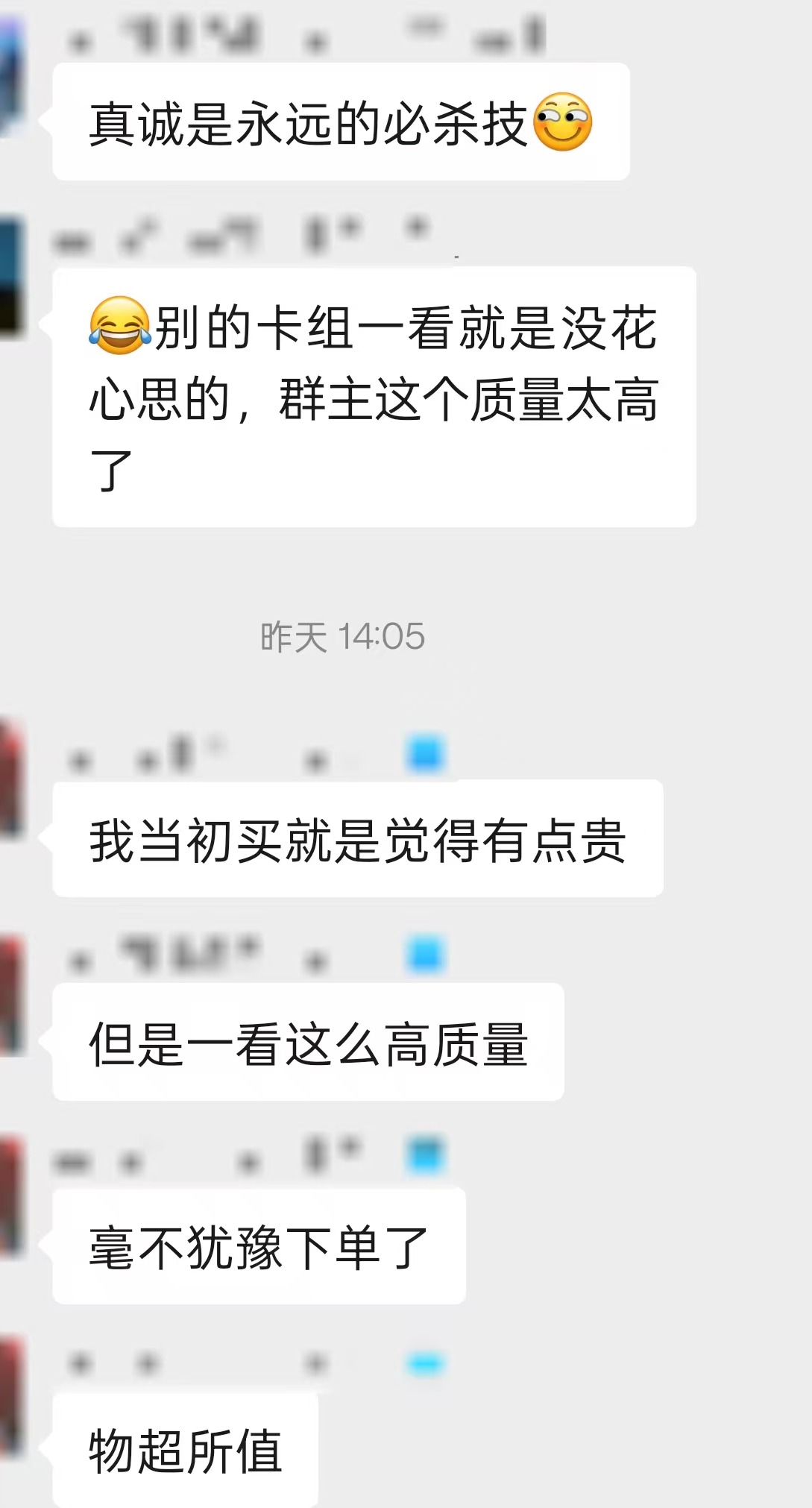
本教程适用于以下云深笔记类卡组
图形推理
数量关系资料分析
成语实词(部分)
申论素材积累(部分)科学推理(广东上海特色)


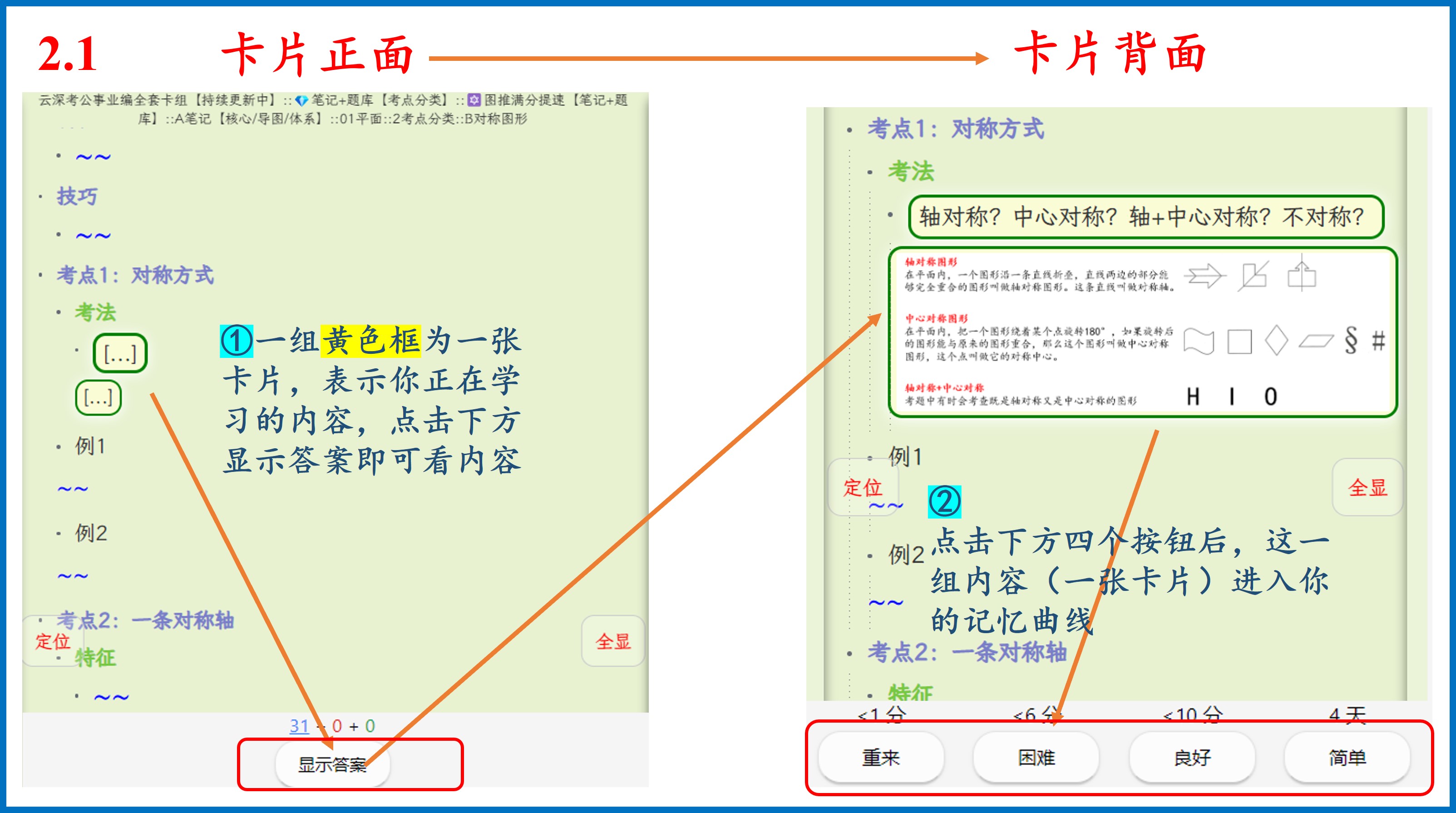

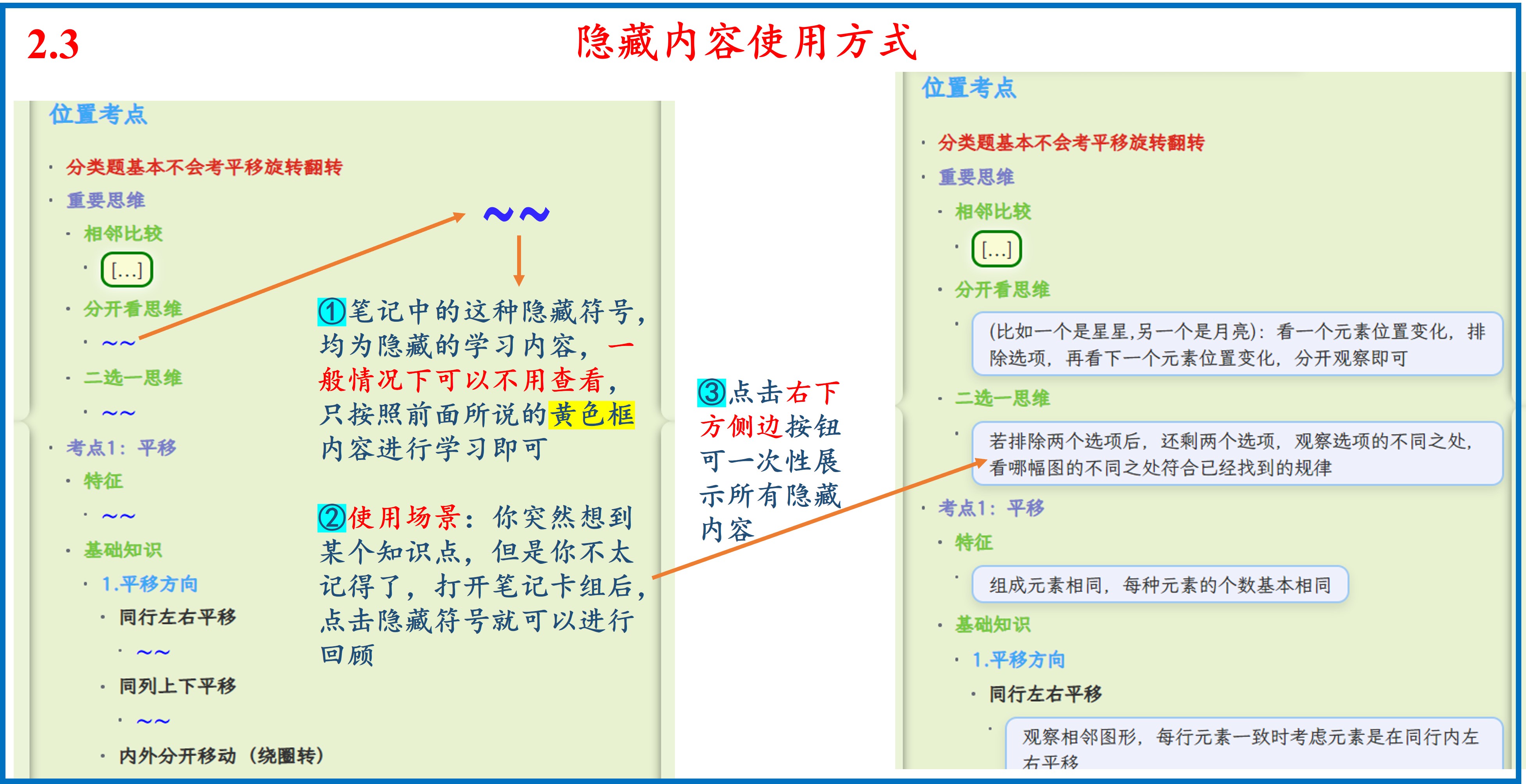

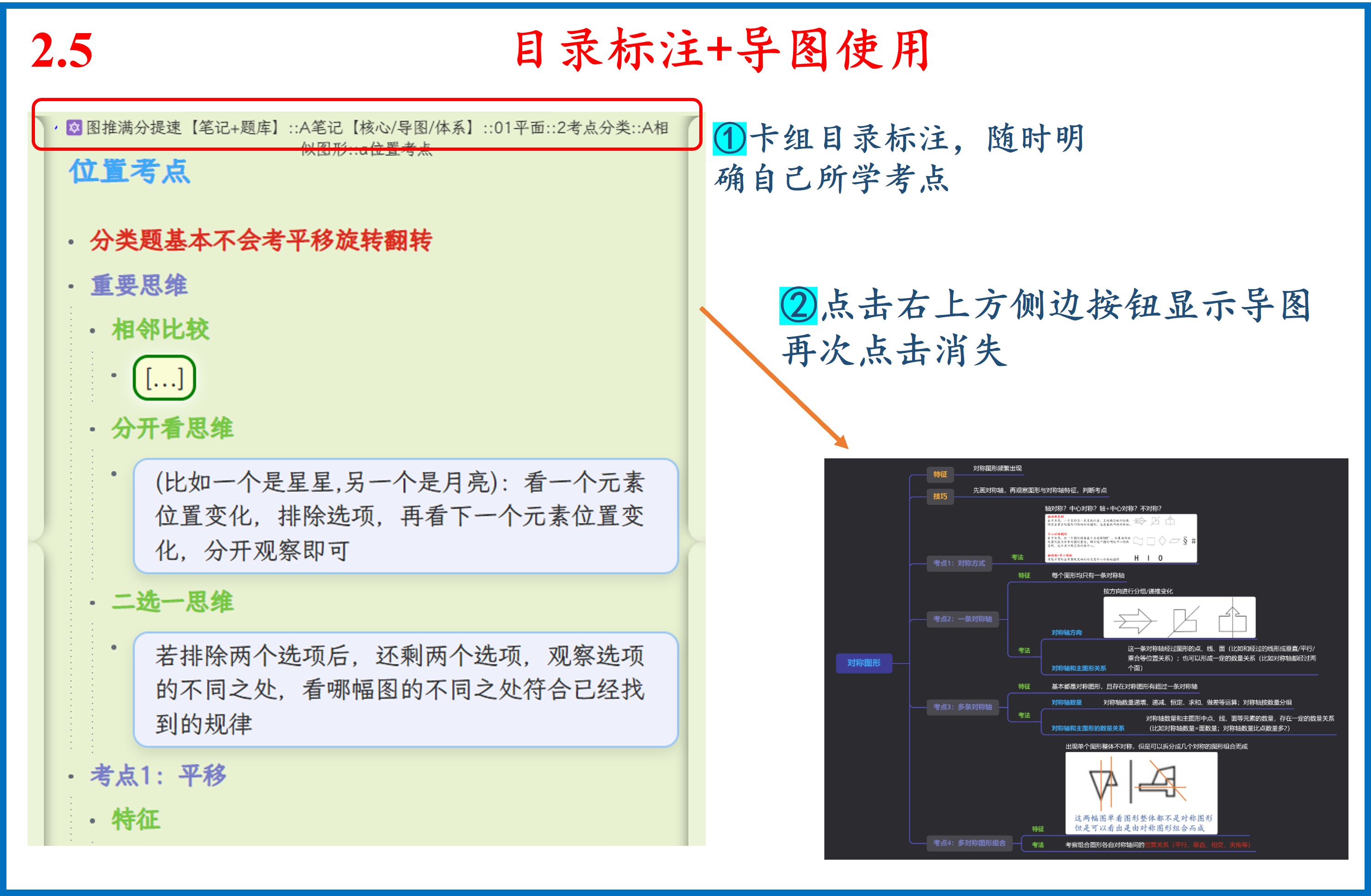
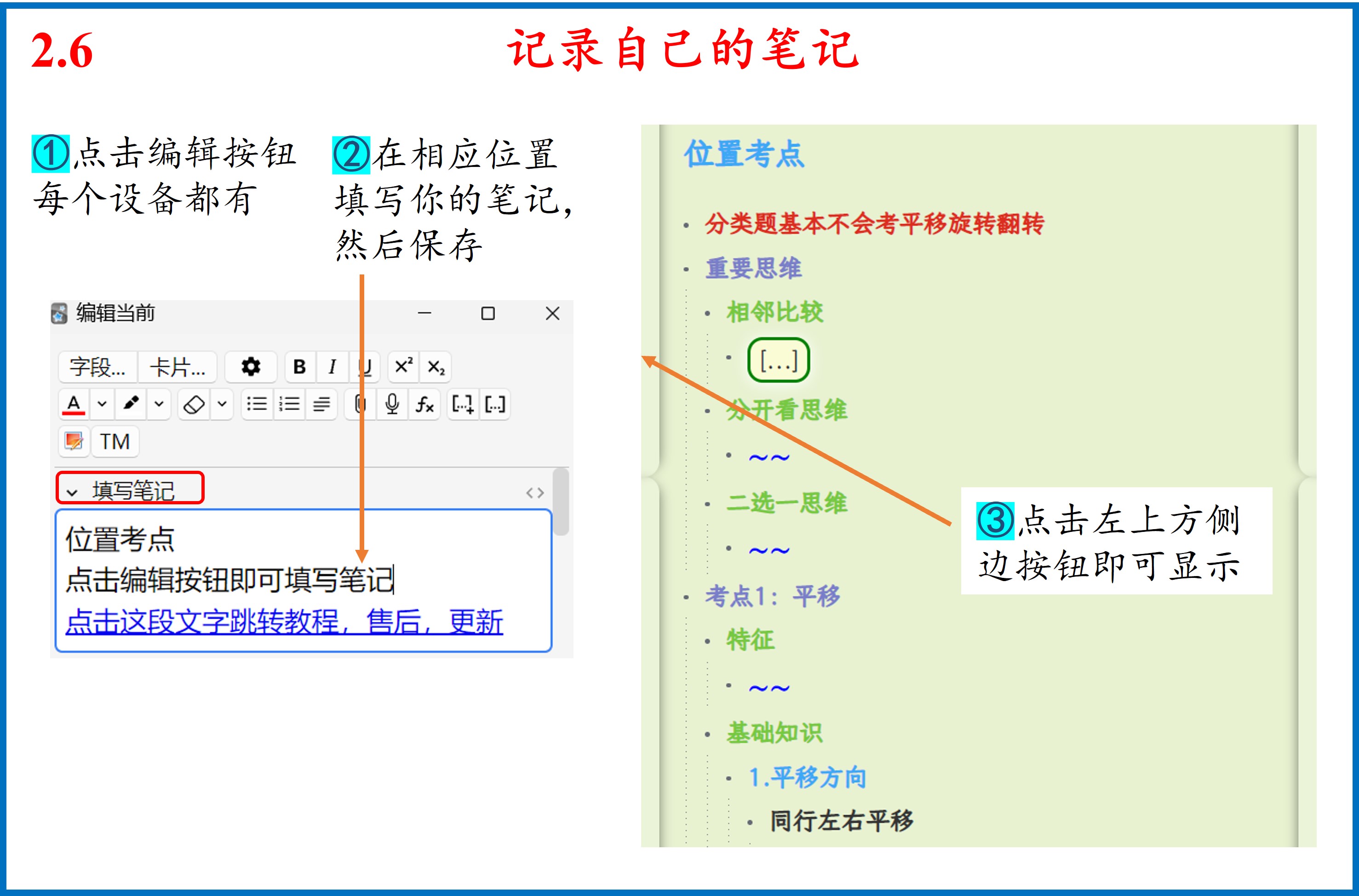
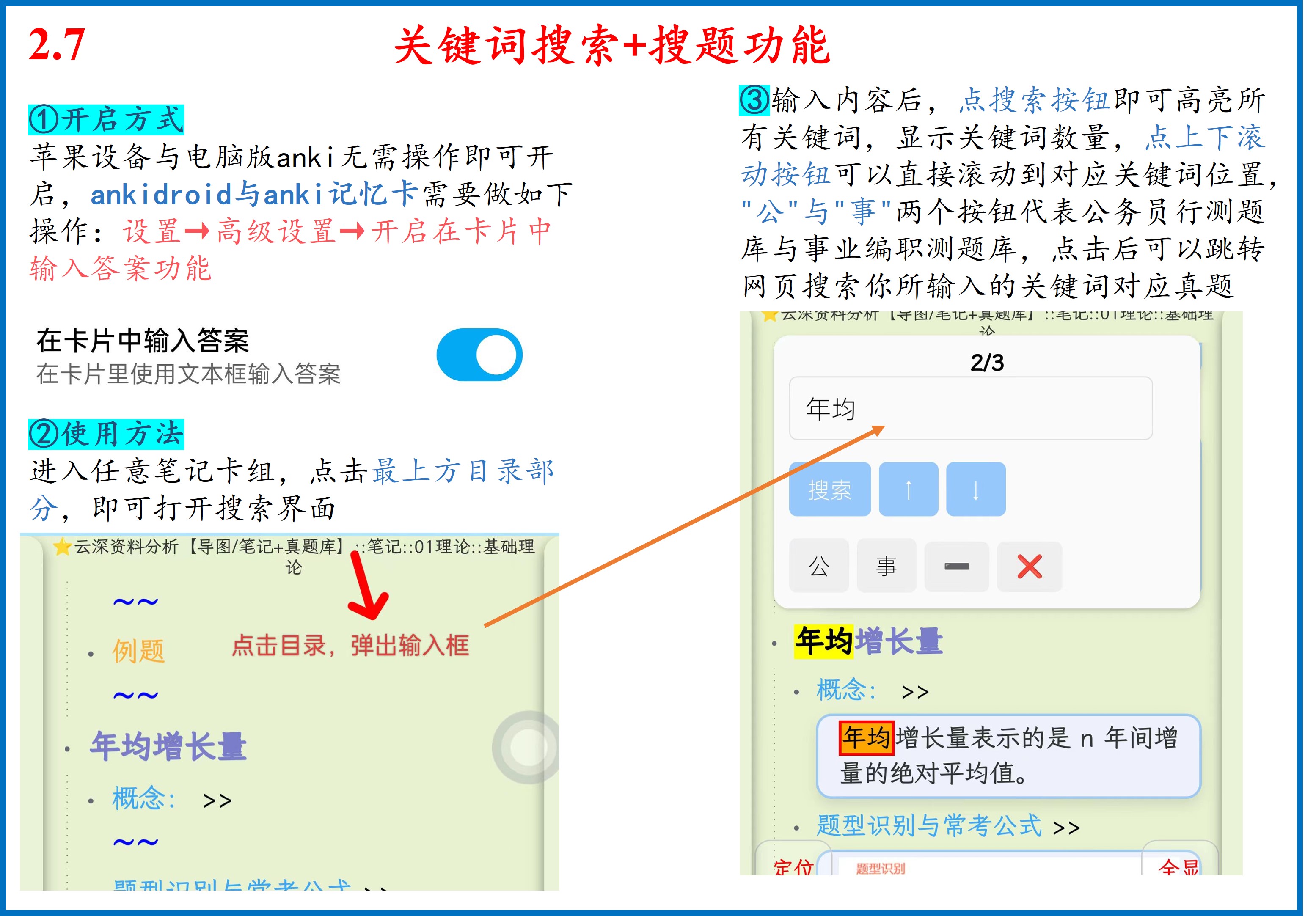
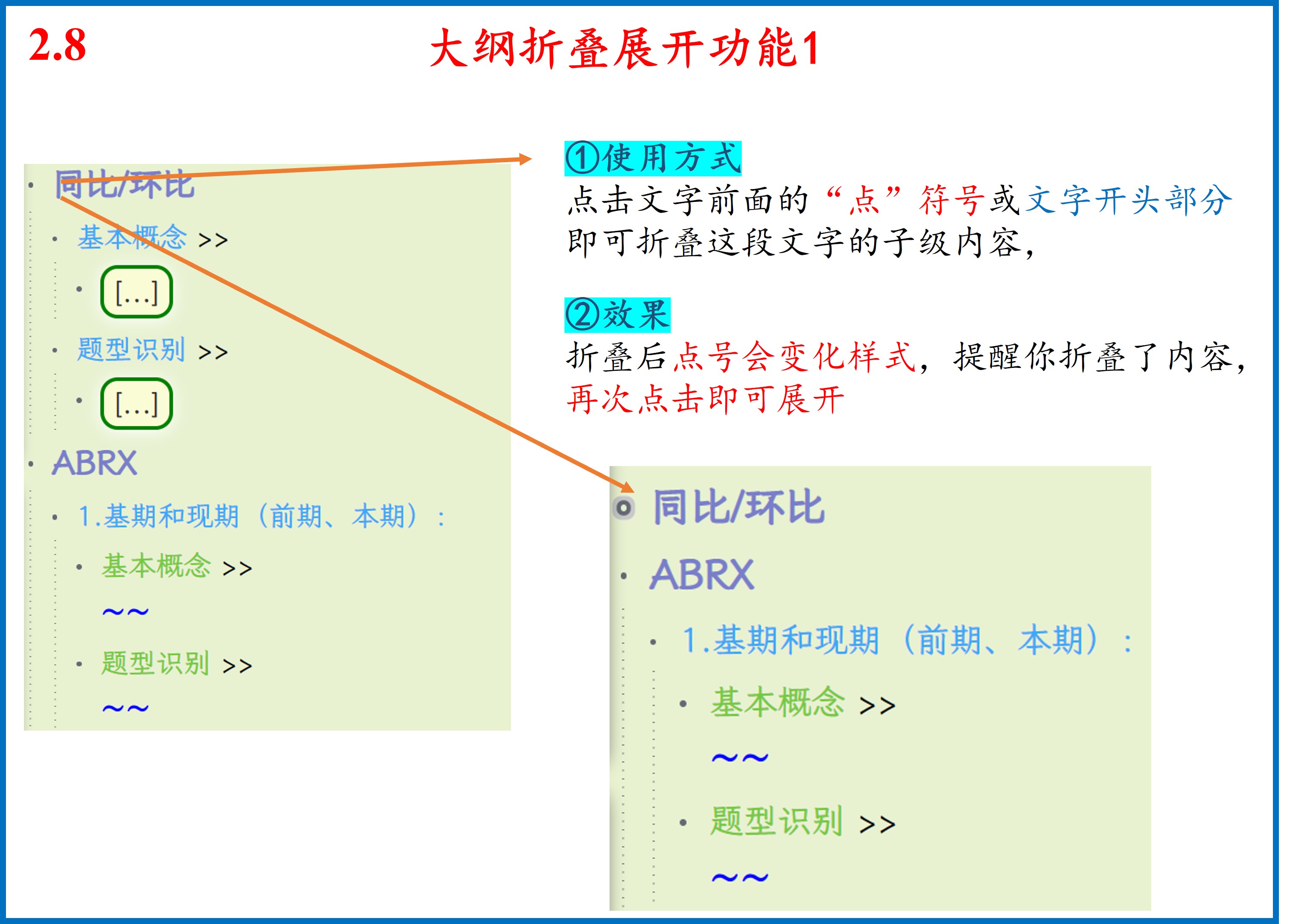
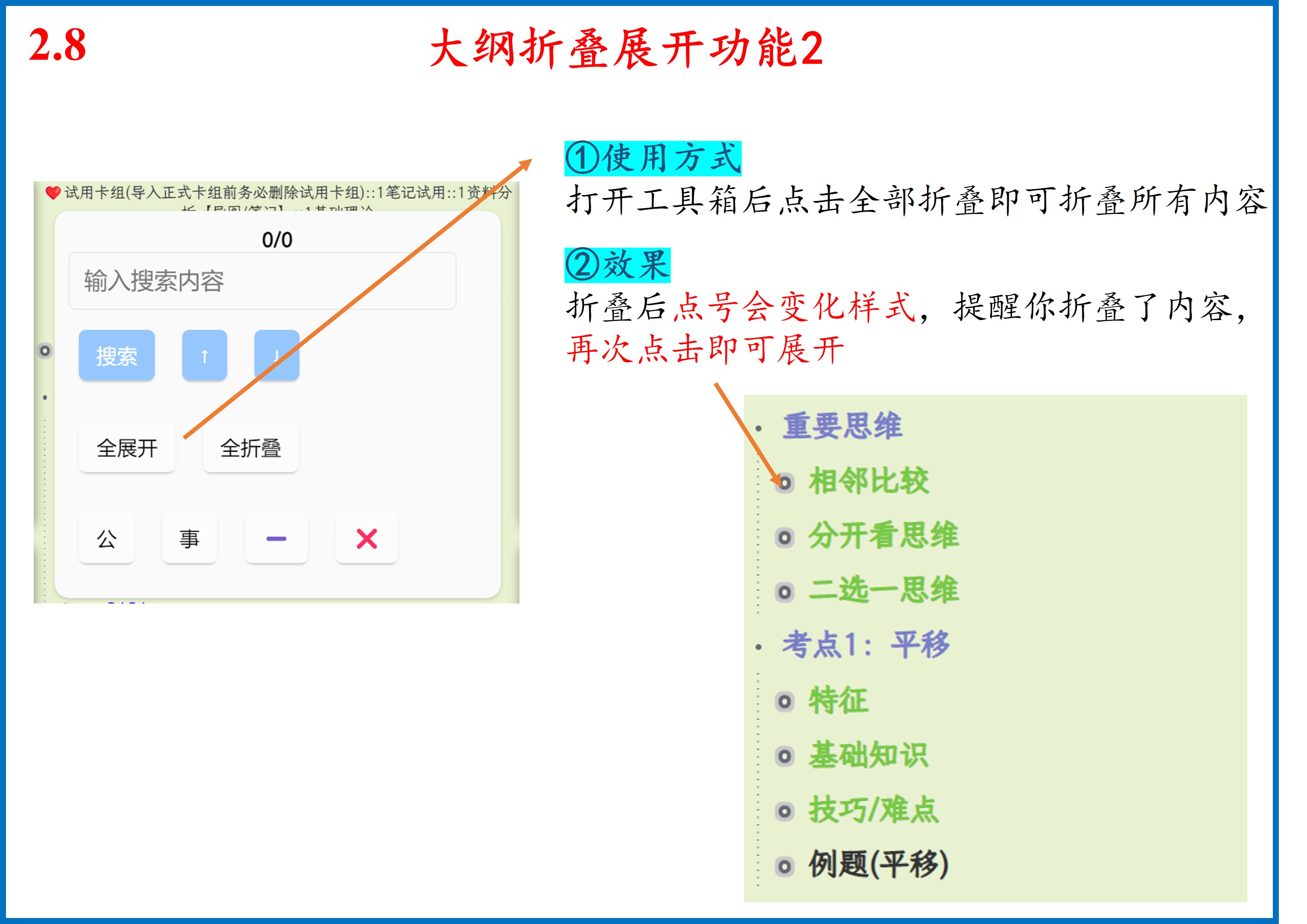
开始您的学习之旅
点击上方目录,可展开查看详细卡组结构
link
下方链接为必看教程,售后,卡组更新日志
长按链接即可复制,浏览器打开链接查看
https://vlink.cc/yunshen
已复制!
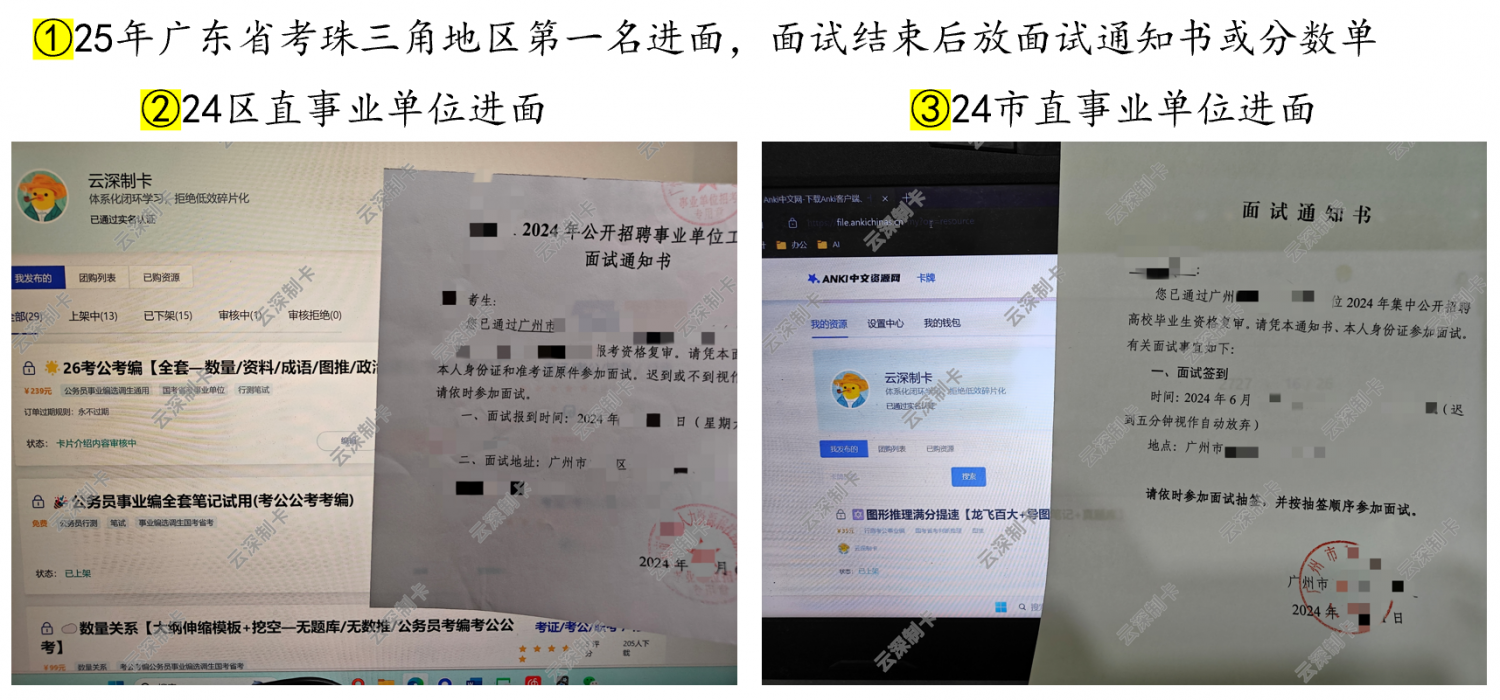


云深制卡 © 真正用心的anki考公卡组制作者
考公系列专属卡组
为考公考编备考者精心设计的学习卡组,覆盖行测、申论等核心考点,真正用心,实战思维制作的卡组,绝非市面批量制作内容可比拟
政治理论+常识速记
政治理论原文来自官方,结合名师讲解笔记,配合独家笔记模板,增加大量内容注释,让你看卡片也能理解实际政策背景和方向,理解性记忆攻克政治理论
常识速记6800条配合学习
visibility查看详情更多学习资源
我们正在整理更多优质学习资源,请持续关注
construction新内容开发中,敬请期待...
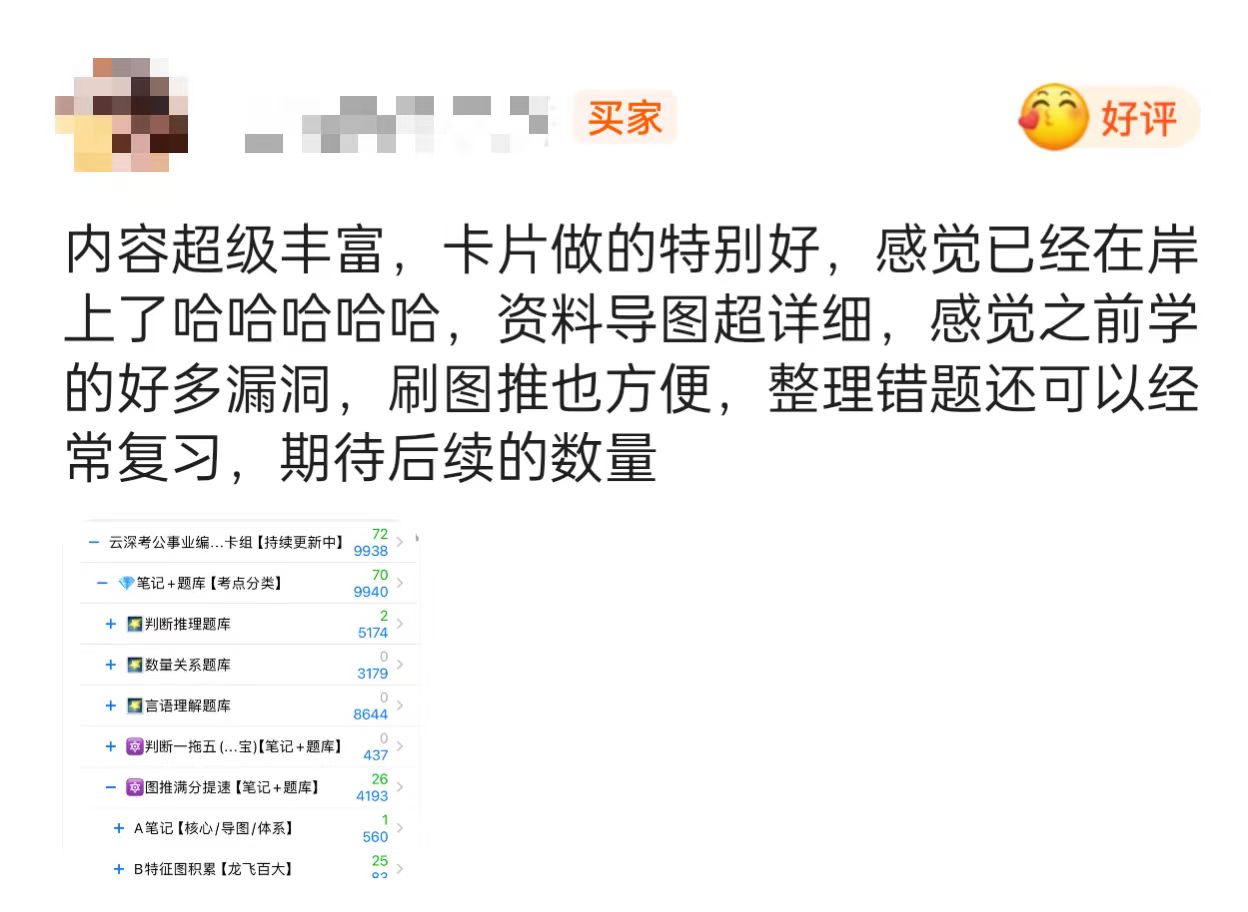
⭐全套笔记卡组
0导读
1
2成语/词语/实词积累2.0
0花生高频【加强版】
【01组】中华文明传统文化
5
【02组】文化传承
8
【03组】改革创新
6
【04组】做法、构思创新
8
【05组】守旧不创新
5
【06组】按规矩办事
6
【07组】处境困难
9
【08组】形势危险
7
【09组】事物出现、发展、衰落
22
【10组】竞争比较
11
【11组】能力不足
10
【12组】印象和效果
9
【13组】搭档配合
8
【14组】工作开展顺序
5
【15组】错误抉择和方向
10
【16组】错误做法 (寓言故事)
11
【17组】教育影响批评
13
【18组】工作学习状态
22
【19组】正确做法
14
【20组】错误做法
7
【21组】某些国家的错误做法
15
【22组】国家安定与动荡
8
【23组】国际国内关系
17
【24组】政府优秀做法
10
【25组】合理规划
5
【26组】政策措施的评价
9
【27组】成功与失败
10
【28组】领导力
16
【29组】正义精神和做法
12
【30组】干部易犯错误
20
【31组】对待错误的态度
12
【32组】改变与不变
19
【33组】顺势造势
6
【34组】自然会发生
6
【35组】提早准备和补救
11
【36组】办公、管理相关
8
【37组】空谈与虚幻
8
【38组】来者众多
11
【39组】人多热闹
6
【40组】好坏掺杂
7
【41组】流行与名声
14
【42组】与传播、传闻相关
11
【43组】与消失、重现相关
14
【44组】明显、含糊相关
12
【45组】重视、重要相关
16
【46组】熟悉、了解、知晓相关
15
【47组】很常见不奇怪
6
【48组】看法一致与否
10
【49组】从细节看全貌
10
【50组】看事情透彻
11
【51组】对事情的态度与评价
7
【52组】数量多与少
11
【53组】建筑相关
6
【54组】相同与不同
17
【55组】技艺精湛
10
【56组】与观看欣赏相关
10
【57组】“说”相关
16
【58组】“演”相关
6
【59组】“听”相关
7
【60组】“写”相关
13
【61组】“钱”相关
9
【62组】“心态”相关
11
【63组】顾忌和无所顾忌
6
【64组】近似成语
24
【65组】生僻成语
8
692
1花生高频【表格版】
【01组】中华文明传统文化
6
【02组】文化传承
9
【03组】改革创新
7
【04组】做法、构思创新
9
【05组】守旧不创新
6
【06组】按规矩办事
7
【07组】处境困难
10
【08组】形势危险
8
【09组】事物出现、发展、衰落
23
【10组】竞争比较
12
【11组】能力不足
11
【12组】印象和效果
10
【13组】搭档配合
9
【14组】工作开展顺序
6
【15组】错误抉择和方向
11
【16组】错误做法 (寓言故事)
12
【17组】教育影响批评
14
【18组】工作学习状态
23
【19组】正确做法
15
【20组】错误做法
8
【21组】某些国家的错误做法
16
【22组】国家安定与动荡
9
【23组】国际国内关系
18
【24组】政府优秀做法
11
【25组】合理规划
6
【26组】政策措施的评价
10
【27组】成功与失败
11
【28组】领导力
17
【29组】正义精神和做法
13
【30组】干部易犯错误
21
【31组】对待错误的态度
13
【32组】改变与不变
20
【33组】顺势造势
7
【34组】自然会发生
7
【35组】提早准备和补救
12
【36组】办公、管理相关
9
【37组】空谈与虚幻
9
【38组】来者众多
12
【39组】人多热闹
7
【40组】好坏掺杂
8
【41组】流行与名声
15
【42组】与传播、传闻相关
12
【43组】与消失、重现相关
15
【44组】明显、含糊相关
13
【45组】重视、重要相关
17
【46组】熟悉、了解、知晓相关
16
【47组】很常见不奇怪
7
【48组】看法一致与否
11
【49组】从细节看全貌
11
【50组】看事情透彻
12
【51组】对事情的态度与评价
8
【52组】数量多与少
12
【53组】建筑相关
7
【54组】相同与不同
18
【55组】技艺精湛
11
【56组】与观看欣赏相关
11
【57组】“说”相关
17
【58组】“演”相关
7
【59组】“听”相关
8
【60组】“写”相关
14
【61组】“钱”相关
10
【62组】“心态”相关
12
【63组】顾忌和无所顾忌
7
【64组】近似成语
25
【65组】生僻成语
9
757
2易错成语分类
1望文生义
A组
155
B组
160
315
2语义重复
126
3对象误用
A组
179
B组
200
379
4双重意义
92
5特殊用法
A用在否定句或疑问句
19
B不能带宾语的成语
53
72
6谦辞敬辞
A敬辞
9
B谦辞
44
53
7褒贬误用
A贬义误作褒用
62
B褒义误作贬用
21
83
8易混误用
145
1265
2老闻实词分组
72
3易错实词
389
4易错虚词
46
5基础成语补充
315
实词分类积累(备注使用语境)
01组
55
02组
55
03组
50
04组
52
05组
62
06组
63
07组
58
08组
58
09组
36
10组
60
11组
64
12组
55
668
成语分类积累(备注使用语境)
01组
59
02组
61
03组
56
04组
57
05组
59
06组
62
07组
61
08组
72
09组
59
10组
61
11组
51
12组
52
13组
61
14组
61
15组
63
16组
39
17组
45
18组
55
19组
55
20组
55
21组
53
22组
50
23组
42
1289
5493
3图推满分提速【3.0】
A笔记【核心/导图/体系】
00⭐图推思路【先看】
1
01平面
1整体框架
14
A相似图形
a位置考点
56
b样式考点
52
c黑白球/块
73
181
B对称图形
31
C结构图形
a相接/相交/上下结构
26
b内外结构
24
50
D多线条图形
0整体思路
4
a曲
23
b面
29
c角
13
d线
43
e点
14
126
E特殊图形
a黑白考点(非相似)
23
b生活化/粗线条
28
c元素形状/数量
28
d元素位置
41
e字类
31
151
553
02立体
截面图
10
10
564
B龙飞百大【25版2.0】
01图形规则类(对称图形)
14
02图形出头类(不完全封闭)
14
03封闭图形类(纯封闭图形)
33
04分离图形类(元素样式)
12
05轮廓类
27
06黑白元素类
17
07特殊元素类
14
08复合考法类
15
09图形修正类
29
175
C龙飞百大【24版1.0】
01组
26
02组
26
03组
11
04组
12
05组
11
06组
11
07组
11
108
847
4申论系列
1规范词(搜词版)
A基础分类
1行政管理类
149
2经济发展类
202
3人文建设类
84
4民生建设类
126
5生态环保类
36
6区域发展类
61
7科技创新类
40
8法律制度
25
723
B现象/问题/原因/对策
具体表现类
基层
140
文化
55
法律
15
生态
28
社会
88
科技
20
经济
97
443
存在问题类
229
解决对策类
266
造成原因类
40
978
C机关工作分类
a基本维度
1.思想、意识、观念、道德类
47
2.法律法规、制度、体制机制类
9
3.人、财、物等资源配置类
45
4.调查研究、组织协调和执法、执行类
35
5.监督监管和群众反馈类
21
6.总结经验、借鉴经验类
29
186
b基本领域
1.行政执法(政府管理)类
45
2.经济类
43
3.文化类
21
4.社会类
34
5.生态类
16
6.乡镇类
63
222
c补充
90
498
2199
1规范词(表格版)
A基础分类
1行政管理类
161
2经济发展类
210
3人文建设类
88
4民生建设类
131
5生态环保类
37
6区域发展类
64
7科技创新类
42
8法律制度
29
762
B现象/问题/原因/对策
a具体表现
1基层类
141
2科技类
21
3社会类
89
4文化类
56
5生态类
29
6经济类
98
7法律类
16
450
b存在问题
230
c造成原因
40
d解决对策
267
987
C机关工作分类
a基本维度
1.思想、意识、观念、道德类
50
2.法律法规、制度、体制机制类
10
3.人、财、物等资源配置类
47
4.调查研究、组织协调和执法、执行类
36
5.监督监管和群众反馈类
24
6.总结经验、借鉴经验类
30
197
b基本领域
1.行政执法(政府管理)类
47
2.经济类
44
3.文化类
22
4.社会类
35
5.生态类
17
6.乡镇类
65
230
c补充
92
519
D细致专题分类
01产业发展
67
02城市建设
57
03法治建设
48
04高质量发展
41
05基层治理
17
06教育建设
60
07科技发展
38
08农业发展
74
09人才培养
30
10体育发展
33
11文化保护
26
12乡村振兴
41
13医疗建设
35
14社会治理
30
15经济发展
24
16加强民生建设
21
17精神文明
7
18政府管理
71
19文化产业
25
20企业管理
49
794
3062
2常用主题模板
01 伟大的新时代
22
02 中国式现代化
18
03 全面深化改革
18
04 党的全面领导
23
05 新时代的青年
26
06 高质量发展
27
07 乡村振兴
29
08 民生福祉
29
09 法治专项
34
10 文化自信
14
11 社会治理
25
12 生态文明
26
291
3经典论据背诵
112
4分类素材积累
01 爱国篇
13
02 爱民·群众篇
7
03 严格执法篇
5
04 诚信篇
10
05 修身篇
9
06 合作与团结篇
8
07 谦虚篇
6
08 奉献篇
8
09 磨难篇
14
10 意志篇
10
11 勤奋篇
13
12 务实篇
6
13 成功篇
11
14 德行篇
6
15 正直篇
11
16 理想篇
8
17 知识篇
9
18 自信篇
7
19 机遇篇
3
20 劳动篇
6
21 读书篇
9
22 竞争篇
6
23 交友篇
9
194
5领导讲话金句
1提振经济
4
2民生建设
4
3脱贫攻坚
4
4乡村建设
4
5生态环保
4
6人文建设
4
24
5882
公基常识
0使用导读
1
【笔记版】
法律
01法理学
01法的概述
2
2
2
马克思主义原理
01马哲
01哲学概述
02哲学和马哲
3
3
3
3
5
【速记版】
4000问
4519
分类记忆
公文
61
历史
288
地理
254
政治
1马克思主义原理
67
2毛思想概论
30
3中国特色社会主义
75
4中共党史
33
205
文学
467
法律
1法理学
97
2宪法
208
3刑法
84
4行政法与行政诉讼法
188
5民法典
178
6劳动合社会保障法
134
889
科技
600
管理学
90
经济学
70
2924
7443
马克108专题
01爱眼
8
02安全用电
4
03报刊
12
04博物馆与文物
01国内国际博物馆地位
6
02博物馆与重要文物对应
18
03中国十大传世名画
15
39
05茶文化
20
06瓷器
12
07磁场与电磁波
13
08大运河
7
09档案馆藏与古代建筑
18
10德国
13
11喀斯特地貌
11
12地质年代
7
13电影及其他世界奖项
26
14俄罗斯
39
15二十四节气
24
16法国文化元素
34
17公益诉讼
7
18古代乐器
16
19古代年龄的别称
33
20古代时间月份别称
40
21古代著名医师
19
22官职变动、古代文书、左右礼仪
33
23航天史上的首次
10
24家庭家风
18
25江西
20
26解法战争
5
27金属之最
18
506
7955
判断
判断一拖五(大宝小宝)
0使用指南
1
1题型及思路
10
2解题详细步骤
37
48
类比推理
00导读
1
01语义/涵义
01近义反义
35
02比喻象征
11
03一字多义
9
55
02范围/逻辑
01全同
13
02并列
41
03包含
31
04交叉
10
95
03对应关系
01原材料/工艺/工具/成品
21
02功能
14
03属性
11
04动作排序
9
05因果
16
06方式目的
14
06条件
14
07其他对应
21
120
04语法关系
16
287
335
政治理论笔记
1党的创新理论(基础核心)
00导论
1习近平新时代中国特色社会主义思想创立的时代背景
1
2习近平新时代中国特色社会主义思想是“两个结合”的重大成果
5
3习近平新时代中国特色社会主义思想是完整的科学体系
3
4习近平新时代中国特色社会主义思想的历史地位
1
5深刻领悟“两个确立”的决定性意义
1
11
01新时代坚持和发展中国特色社会主义
1方向决定道路,道路决定命运
6
2中国特色社会主义进入新时代
7
13
02以中国式现代化全面推进中华民族伟大复兴
1实现中华民族伟大复兴的中国梦
1
2全面建成社会主义现代化强国
2
3中国式现代化
6
10
03坚持党的全面领导
1中国共产党领导是中国特色社会主义最本质的特征
3
2坚持中国共产党对一切工作的领导
3
3健全和完善党的领导制度体系
3
9
04坚持以人民为中心
1江山就是人民,人民就是江山
3
2坚持人民至上
4
3全面落实以人民为中心的发展思想
6
14
05全面深化改革开放
1改革开放是决定当代中国命运的关键一招
5
2统筹推进各领域各方面改革开放
3
3将改革开放进行到底
3
11
06推动高质量发展
1完整、准确、全面贯彻新发展理念
7
2坚持和完善社会主义基本经济制度
7
3加快构建新发展格局
7
4建设现代化经济体系
4
26
07社会主义现代化建设的教育、科技、人才战略
1全面建设社会主义现代化国家的基础性、战略性支撑
3
2加快建设教育强国
4
3加快建设科技强国
6
4加快建设人才强国
3
16
08发展全过程人民民主(考察少)
1坚定中国特色社会主义政治制度自信
4
2全过程人民民主是社会主义民主政治的本质属性
6
3健全人民当家作主的制度体系
11
4巩固和发展新时代爱国统一战线
7
28
09全面依法治国(侧重考细致法律常识)
1坚持中国特色社会主义法治道路
5
2建设中国特色社会主义法治体系
3
3加快建设法治中国
4
12
10建设社会主义文化强国
1文化是民族生存和发展的重要力量
9
2建设具有强大凝聚力和引领力的社会主义意识形态
4
3以社会主义核心价值观引领文化建设
3
4铸就社会主义文化新辉煌(重要考点)
7
23
11以保障和改善民生为重点加强社会建设
1让人民生活幸福是“国之大者 ”
4
2不断提高人民生活品质
5
3在共建共治共享中推进社会治理现代化
8
17
12建设社会主义生态文明
1坚持人与自然和谐共生
6
2建设美丽中国
10
16
13维护和塑造国家安全
1坚持总体国家安全观
5
2构建统筹各领域安全的新安全格局
9
3开创新时代国家安全工作新局面
3
17
14建设巩固国防和强大人民军队(考察少)
1强国必须强军,军强才能国安
3
2实现党在新时代的强军目标⭐
6
3加快推进国防和军队现代化
4
13
15坚持“一国两制”和推进祖国完全统一
1全面准确理解和贯彻“一国两制”方针
10
2保持香港、澳门长期繁荣稳定
2
3推进祖国完全统一
4
16
16中国特色大国外交和推动构建人类命运共同体
1新时代中国外交在大变局中开创新局
3
2全面推进中国特色大国外交
4
3推动构建人类命运共同体
8
15
17全面从严治党⭐⭐
1全面从严治党是新时代党的建设的鲜明主题
4
2以政治建设为统领深入推进党的建设
8
3坚定不移推进反腐败斗争
4
4建设长期执政的马克思主义政党
5
21
288
2党和国家方针政策(重点)
00整体导读
1
01重要会议
1、二十届三中全会(24年7月)
0导论
4
1进一步全面深化改革的重要性和必要性
1
2进一步全面深化改革的指导思想
1
3进一步全面深化改革的总目标
1
4进一步全面深化改革的重大原则
1
5进一步全面深化改革的系统部署
1
9
2、中央经济会议(24年12月)
1我们不断深化对经济工作的规律性认识
1
2做好明年经济工作的总体要求和政策取向
2
3明年要抓好以下重点任务
9
13
3、政府工作报告(25年3月)
01【24年工作回顾】
13
02【25年经济社会发展总体要求和政策取向】
7
03【25年政府工作任务】
01大力提振消费 、提高投资效益,全方位扩大国内需求
2
02因地制宜发展新质生产力,加快建设现代化产业体系
4
03深入实施科教兴国战略,提升国家创新体系整体效能
4
04推动标志性改革举措加快落地,更好发挥经济体制改革牵引作用
4
05扩大高水平对外开放,积极稳外贸稳外资
5
06有效防范化解重点领域风险,牢牢守住不发生系统性风险底线
4
07着力抓好“三农”工作,深入推进乡村全面振兴
1
08推进新型城镇化和区域协调发展,进一步优化发展空间格局
3
09推进新型城镇化和区域协调发展,进一步优化发展空间格局
1
10加大保障和改善民生力度,提升社会治理效能
6
34
54
76
02周年纪念
24.08邓小平同志诞辰120周年
6
24.09中华人民共和国成立75周年
1
24.09中国人民政治协商会议成立75周年
5
24.09全国人民代表大会成立70周年
4
24.12澳门回归祖国二十五周年
3
19
03经济建设
1新质生产力
24.02中共中央政治局就扎实推进高质量发展进行第十一次集体学习
7
24.07二十届三中全会
1
8
2科技强国
24.06嫦娥六号
1
24.07二十届三中全会
1
25.04中共中央政治局第二十次集体学习
1
3
3金融强国
23.10中央金融工作会议
3
24.01习近平在省部级主要领导干部推动金融高质量发展专题研讨班开班式上发表重要讲话
2
5
4高水平社会主义市场经济体制
24.07二十届三中全会
2
24.08关于完善市场准入制度的意见
1
25.02民营企业座谈会
6
25.04《中华人民共和国民营经济促进法》
1
25.04中共中央政治局会议
8
25.05《关于健全资源环境要素市场化配置体系的意见》
2
25.05《关于完善中国特色现代企业制度的意见》印发
2
25.05国务院召开做强国内大循环工作推进会
1
23
5高水平对外开放体制机制
24.09《国务院办公厅关于以高水平开放推动服务贸易高质量发展的意见》
1
1
6区域发展
24.03新时代推动中部地区崛起座谈会
1
24.04新时代推动西部大开发座谈会
1
25.01习近平总书记辽宁考察重要讲话
1
25.02习近平在听取吉林省委和省政府工作汇报时的重要讲话
1
25.03习近平在云南考察
2
25.03习近平在贵州考察
2
8
7乡村振兴
24.12中央农村会议
1
25.01《乡村全面振兴规划 (2024—2027年) 》
5
25.02中央一号文件
32
25.04《加快建设农业强国规划(2024-2035年)》
18
56
104
04政治建设
0导读
1
1统一战线
24.07二十届三中全会
1
1
2民族团结
24.09习近平在全国民族团结进步表彰大会上的讲话
4
4
3“一国两制”与祖国统一
24.03香港国安条例
1
24.04习近平会见马英九一行
2
24.06《关于依法惩治“台独”顽固分子分裂国家、煽动分裂国家犯罪的意见》
1
4
4国家安全
25.02中共中央政治局第十九次集体学习
1
25.05《新时代的中国国家安全》白皮书发布
3
4
14
05文化建设
23.10全国宣传思想文化工作会议
1
24.07二十届三中全会
1
2
06社会建设
1教育
24.08加强新时代高素质专业化教师队伍建设的意见
1
24.09全国教育大会
5
25.01《教育强国建设规划纲要 (2024—2035年) 》
3
9
2体育
24.08习近平接见第33届奥运会中国体育代表团
1
1
3就业
24.09实施就业优先战略
3
3
4人口
24.09《关于实施渐进式延迟法定退休年龄的决定 》
1
1
5其他
25.05《中办、国办印发关于持续推进城市更新行动的意见》印发
1
1
15
07生态文明建设
24.03习近平主持中共中央政治局第十二次集体学习
1
24.07二十届三中全会
1
24.08《中国的能源转型》白皮书
1
24.08《关于加快经济社会发展全面绿色转型的意见》
5
24.09黄河流域生态保护和高质量发展座谈会
1
25.05《美丽河湖保护与建设行动方案(2025—2027年)》
1
10
08党的建设⭐
1深化党的建设制度改革
24.07二十届三中全会
1
1
2深入推进党的自我革命
24.01习近平在党的第二十届中央纪律检查委员会第三次全体会议上讲话
3
3
3全面从严治党
24.06中共中央政治局就健全全面从严治党体系进行第十五次集体学习
1
1
4党的纪律
24.04《关于在全党开展党纪学习教育的通知》
1
24.12中共中央政治局民主生活会
1
25.05《党政机关厉行节约反对浪费条例》
3
5
二十届中央纪委四次全会(25.01)
8
18
09大国外交
24.06和平共处五项原则发表 70 周年
6
24.09中非合作论坛峰会
5
24.12第四次“一带一路”建设工作座谈会
1
25.05习近平在《俄罗斯报》发表《以史为鉴共创未来》
4
25.05习近平在中拉共同体论坛上的讲话
1
17
10《求是》文章
24.11《求是24年22期》以人口高质量发展支撑中国式现代化
2
25.01《求是25年01期》以中国式现代化全面推进强国建设、民族复兴伟业
1
25.01《求是25年02期》进一步全面深化改革中的几个重大理论和实践问题
1
25.02《求是25年03期》注重家庭,注重家教,注重家风
1
25.02《求是25年04期》健全全面从严治党体系
1
25.03《求是25年05期》经济工作必须统筹好几对重要关系
1
25.03《求是25年06期》坚持和落实“两个毫不动摇”
3
25.04《求是25年07期》朝着建成科技强国的宏伟目标奋勇前进
5
25.04《求是25年08期》 加快建设文化强国
2
25.05《求是25年09期》 激励新时代青年在中国式现代化建设中挺膺担当
4
25.05《求是25年10期》 锲而不舍落实中央八项规定精神,以优良党风引领社风民风
4
25
301
589
政治理论题库
00解题思维【真题】
国考
24国考
11
25国考
20
31
省考(筛选出通用的考题)
四川
9
天津
4
浙江
10
23
54
0笔记配套题库【推荐】
1党的创新理论
01导论
7
02新时代坚持和发展中国特色社会主义
5
03以中国式现代化全面推进中华民族伟大复兴
3
04坚持党的全面领导
2
05坚持以人民为中心
4
06全面深化改革开放
6
07推动高质量发展
11
08社会主义现代化建设的教育、 科技、 人才战略
5
09发展全过程人民民主
9
10全面依法治国
3
11建设社会主义文化强国
8
12以保障和改善民生为重点加强社会建设
9
13建设社会主义生态文明
5
14维护和塑造国家安全
5
15建设和巩固国防和强大人民军队
3
16坚持“一国两制” 和推进祖国完全统一
5
17中国特色大国外交推动构建人类命运共同体
4
18全面从严治党
6
100
2时政方针
01重要会议
1二十届三中全会
11
2中央经济会议
8
19
02周年纪念
1习近平在庆祝中华人民共和国成立 75 周年招待会上的讲话
1
2习近平在庆祝全国人民代表大会成立 70 周年大会上的讲话
2
3习近平在庆祝中国人民政治协商会议成立 75 周年大会上的讲话
4
4习近平在纪念邓小平同志诞辰 120 周年座谈会上的讲话
2
9
03经济建设
1新质生产力
8
2科技强国
6
3金融强国
5
4高水平社会主义市场经济体制
4
5高水平对外开放体制机制
2
6区域发展
3
7乡村振兴
4
32
04政治建设
7
05文化建设
3
06社会建设
9
07生态文明建设
7
08党的建设
8
09大国外交
6
100
200
1机构题库
01CG
200【新】
200
200【旧】
198
25多省联考事业编
50
25广东事业编统考
80
中央经济工作会议
20
考前冲刺
【24年国考】
中共中央、国务院会议
6
中共中央、国务院方针政策
14
习近平新时代中国特色社会主义思想
6
习近平讲话与《求是》文章
15
二十届三中全会
9
50
【315省考】
50
100
648
02LMJ
选择
单选
150
多选
47
197
197
03ZG
党和国家方针政策 100 题
100
党的创新理论
100
200
1045
1299
月度时政【常识】
0导读
1
25年
01月
54
02月
39
03月
58
04月
69
05月
67
287
288
每月时政模拟题
24年
01月模拟
76
02月模拟
75
03月模拟
63
04月模拟
72
05月模拟
76
06月模拟
89
07月模拟
70
08月模拟
59
09月模拟
77
10月模拟
73
11月模拟
52
12月模拟
66
848
25年
01-02月
69
03月
120
04月
120
05月
120
429
1277
23966
暂无预览
版权声明:平台资源均由用户制作上传,若存在侵权行为,请发送反馈信件至ankimemory@163.com联系平台进行处理,感谢理解!
作者其他资源
公基4万4千题
考证/考公/职考 / 行测
¥10元 公基常识
事业编三支一扶
 云深制卡
云深制卡
评分积累中
26类比推理笔记导图【大纲伸缩模板+挖空—无题库/公务员考编考公公考】
考证/考公/职考 / 行测
¥20元 考公事业编国考省考选调生
行测职测
 云深制卡
云深制卡
5 评分
26公基常识笔记版【预售】考公事业编公考事考
考证/考公/职考 / 行测
¥9999元 公务员
公务员考试
公务员行测
 云深制卡
云深制卡
评分积累中
26政治理论笔记题库+常识公基速记+公基四万真题+每月时政(持续更新)
考证/考公/职考 / 行测
¥50元 政治理论
【云深制卡】
 云深制卡
云深制卡
5 评分
26政治理论笔记题库+常识公基速记+公基四万真题+每月时政(持续更新)
考证/考公/职考 / 行测
¥50元 政治理论
【云深制卡】
 云深制卡
云深制卡
4.9 评分
积分不足!
下载消耗1积分
请使用APP下载
充值积分
该商品属于虚拟商品,购买后将无法退款,请确认后购买
请输入兑换码
请打开微信扫码拼团
选择喜欢的内容
